Abstract
Significance: Biological tissues are typically characterized by high anisotropic scattering and may also exhibit linear form birefringence. Both scattering and birefringence bias the phase shift between transverse electric field components of polarized light. These phase alterations are associated with particular structural malformations in the tissue. In fact, the majority of polarization-based techniques are unable to distinguish the nature of the phase shift induced by birefringence or scattering of light.
Aim: We explore the distinct contributions of scattering and birefringence in the phase retardation of circularly polarized light propagated in turbid tissue-like scattering medium.
Approach: The circularly polarized light in frame of Stokes polarimetry approach is used for the screening of biotissue phantoms and chicken skin samples. The change of optical properties in chicken skin is accomplished by optical clearing, which reduces scattering, and mechanical stretch, which induces birefringence. The change of optical properties of skin tissue is confirmed by spectrophotometric measurements and second-harmonic generation imaging.
Results: The contributions of scattering and birefringence in the phase retardation of circularly polarized light propagated in biological tissues are distinguished by the locus of the Stokes vector mapped on the Poincaré sphere. The phase retardation of circularly polarized light due to scattering alterations is assessed. The value of birefringence in chicken skin is estimated as 0.3 × 10− 3, which agrees with alternative studies. The change of birefringence of skin tissue due to mechanical stretch in the order of 10− 6 is detected.
Conclusions: While the polarimetric parameters on their own do not allow distinguishing the contributions of scattering and birefringence, the resultant Stokes vector trajectory on the Poincaré sphere reveals the role of scattering and birefringence in the total phase retardation. The described approach, applied independently or in combination with Mueller polarimetry, can be beneficial for the advanced characterization of various types of malformations within biological tissues.
1.
Introduction
The use of polarized light in various biomedical applications is rapidly growing in the recent years.1 The advantages of polarization-based diagnostic modalities over the conventional optical techniques, as well as the features and challenges of the characterization of biological tissues using so-called optical polarization fingerprint, are widely described elsewhere.2–5 Due to its unique properties, the polarized light is widely used as a considerable add-on to a number of conventional diagnostic and imaging techniques. This addition provides valuable insight on morphological structure of a biotissue. The examples are polarization-sensitive optical coherence tomography,6 polarization-sensitive hyperspectral imaging,7 second-harmonic generation (SHG) polarimetry,8 polarization-sensitive microscopy,9 and others.
The field-based Jones-vector formalism and the intensity-based Stokes–Mueller calculus are the two major mathematical approaches that define the state of polarization of light and describe interaction of polarized light with media.10 A number of innovative polarization-based modalities have been developed for various biomedical applications, utilizing physically measurable Stokes–Mueller parameters, e.g., Mueller-matrix polarimetry.11–14 This approach enables obtaining a complete 4×4 Mueller matrix of the sample that contains full polarimetric information of the examined sample. Mueller-matrix polarimetry shows promising results, in particular, in screening of cancerous tissues15–18 and characterization of other turbid tissue-like scattering media.19–21 Moreover, it has been demonstrated that utilizing circularly polarized light in frame of Stokes-vector polarimetry approach, complemented by the use of Poincaré sphere as a quantitative graphical tool, has a high potential for tissue characterization and evaluation of cancer aggressiveness.22–27
In terms of optical properties, besides absorption, biological tissues are characterized by scattering (typically, in the order of tens of mm−1 for visible light) and high anisotropy of scattering (g≈0.8).28 In addition to scattering of light, due to heterogeneous fibrous structure, biological tissues often exhibit linear form birefringence, which is a measurable quantity; its changes may act as a metric for certain structural abnormalities of biological tissues.29 In fact, both scattering and birefringence may elaborate phase shift between electric field components of the field vector of polarized light during its propagation within the biological medium. Examples of such tissues, cartilage30 or tendon,31 exhibit sufficient form birefringence due to linearly ordered structures,4 and the abnormalities of the structure can be detected fairly easily. On the contrary, skin collagen fibers are characterized by arbitrary orientation,32,33 which makes the birefringence contribution to the phase shift between electric field components of polarized light very minor compared to scattering. This poses a challenge to distinguish birefringence in skin and analyze its changes due to possible structural abnormalities of the tissue. Thus, in the frame of Mueller-matrix polarimetry, it is not possible to distinguish the phase shift between transverse electric field components occurring due to birefringence from one taking place due to light scattering. The aim of the current study is to explore how the variations of birefringence and scattering contribute to the overall phase retardation of circularly polarized light propagated in turbid tissue-like scattering medium, such as skin. We apply laser-based Stokes-vector polarimetry with circularly polarized illumination,22 which is a robust and more cost-effective approach for the tissue characterization than the Mueller-matrix polarimetry. This laser scanning imaging approach ensures better control of light localization within the tissue sample. The advantages of circularly polarized light include directional awareness,34–37 i.e., the flip in helicity in case of backscattering and helicity preservation for forward scattering. This phenomenon, known as the polarization memory of circularly polarized light,34,35,38 is of fundamental importance. Linear polarization possesses no such sense of the direction in which light travels.
In order to systematically investigate the alterations of phase shift between transverse components of circularly polarized light due to scattering and birefringence, we utilize both the phantoms of biological tissues fabricated in-house and tissue samples. The chicken skin was chosen as an example of biological tissue due to the presence of both form and intrinsic birefringence inherent to collagen39,40 as well as scattering.
2.
Methods and Materials
2.1.
Experimental System
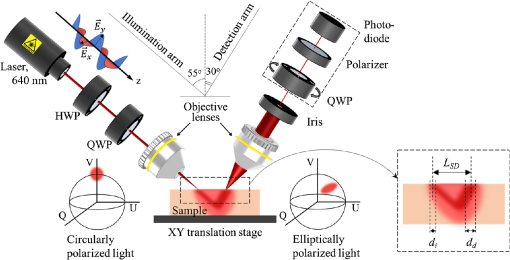
In the experimental system (Fig. 1) developed in-house, the linearly polarized light produced by a laser source (640 nm, Edmund Optics) was altered by half-wave and quarter-wave plates into the right-hand circular polarization. The right-hand circularly polarized light was focused with an objective lens on the sample at 55 deg angle. The sample was placed on the X–Y translation stage. The backscattered light was collected with an objective lens at 30 deg angle at a variable distance LSD away from the point of incidence, vignetted by a 100-μm iris and its state of polarization was analyzed by the Stokes-vector polarimeter (Thorlabs), which consisted of a rotating quarter-wave plate, a polarizer, and a power meter. The diameter of the incident focused laser beam di was ∼15μm [measured with a laser beam profiler (BeamMaster BM-7, Coherent)]. The field of view of the objective lens in the detection arm dd was 50μm. The measured Stokes vectors were analyzed using the Poincaré sphere as a graphical tool.22,26,27,41 In Fig. 1, two Poincaré spheres show, respectively, the position of the Stokes vector of incident right circularly polarized light (sphere on the left) and its relative changes upon interaction with the medium/tissue sample (sphere on the right). The described experimental system has been used extensively in previous studies.22,23,25
2.2.
Experimental Protocols
In order to explore the contributions of scattering and birefringence to the phase retardation of circularly polarized light, a series of experiments with biotissue-mimicking phantoms and biological tissues has been performed.
2.2.1.
Model experiments
Variation of source–detector separation. In order to confirm the impact of the source–detector separation LSDon the state of polarization of light scattered from a turbid tissue-like scattering medium, an experiment with variation of the source–detector separation was performed utilizing a tissue phantom. The state of polarization of light scattered from the phantom (μs=6mm−1, g≈0.8, and thickness=8mm) was measured with different source–detector separations (−0.05mm≤LSD≤0.7mm). The value of LSD was measured from the estimated zero point, which was the place of coincidence of focal points of the illumination and detection arms, which corresponded to the highest intensity on the detector. The point of coincidence was set as LSD=0; further convergence of the source and detector was considered negative LSD, while their separation was considered positive LSD.
Tissue-mimicking phantoms with the confirmed optical properties at certain wavelengths were fabricated in-house from polyvinyl chloride plastisol (M-F Manufacturing Co.), a white opaque fatty solution of monomers that polymerizes and becomes transparent at high temperatures. ZnO particles (Sigma-Aldrich, Germany) were used to imitate scattering properties assessed based on concentration and size distribution retrieved from the scanning/transmission electron microscopy. The preparation procedure was described elsewhere.42,43 The fabricated phantoms were stored on glass slides at room temperature protected from direct light. The scattering properties of the tissue phantoms were confirmed with the standard measurements of collimated transmittance, total transmittance, and total reflectance43,44 using the spectrophotometric system equipped with integrating spheres OL-750 (Optronic Laboratories) in 600- to 700-nm spectral range. The thickness of samples was measured with the optical coherence tomograph (Hyperion, Thorlabs), whereas the refractive index was estimated with the Abbe refractometer (DR-M2 1550, Atago, Japan).
Alteration of phase of circularly polarized light due to scattering and birefringence. In the model experiments, the change of scattering was achieved by utilizing tissue phantoms with different scattering coefficients (μs=4 and 8mm−1, g≈0.8, thickness=1mm), whereas the phase alteration occurring due to birefringence was mimicked through adding a variable phase shift into incident illumination utilizing the half-wave plate (see Fig. 1). Experiments were performed with LSD=1.5mm. In order to demonstrate the phase alterations due to birefringence in the absence of scattering, a simple experiment with a mirror used as a sample was performed (LSD=0mm and μs=0mm−1; the angles of incidence and detection were changed in order to detect reflection from the mirror).
2.2.2.
Distinguishing scattering and birefringence in phase alterations using chicken skin
In order to differentiate the contributions of scattering and birefringence in the phase retardation of polarized light propagated through the chicken skin, optical clearing45,46 was used to suppress scattering, whereas birefringence was induced by mechanical stretch. A separate measurement of the scattering properties of the chicken skin tissue with and without clearing was performed using the spectrophotometric system, as described in Sec. 2.2.1. Optical clearing was performed by applying 40% glycerol solution in water during 1 h. Alignment of collagen fibers in optically cleared chicken skin as a result of mechanical stretch was validated separately by the SHG imaging utilizing standard multiphoton microscope (A1R MP+, Nikon). The imaging was performed using CFI Plan Apochromat 10× G Glyc objective (corrected for water and glycerol) immersed in 40% glycerol-water solution without a cover glass.
Based on the findings acquired in the model experiments and SHG imaging of collagen fibers in chicken skin, three-stage experiments with samples of chicken skin were performed. The sample of chicken skin (size, ∼2.5×6.5cm2) was excised from a chicken thigh and placed on a sample holder with the inner side of the skin up. To exclude the scattering on the roughness of skin and surface contaminations caused by flakes and/or fractions of residual feather follicles, the samples of chicken skin were measured from the inner side. The spatial scanning of the tissue sample was performed at the 2×2mm2 surface area with a 200-μmstep. The measurement at each scanning point was an average of 10 measurements. At the first stage, the sample was left intact for 30 min under normal conditions for reducing the level of humidity on the surface of the freshly excised sample. Further, the optical clearing agent (40% glycerol-water solution) was applied topically to the surface of the sample. After 60 min of optical clearing, the mechanical stretch (up to1.5 N) was gradually applied to the optically cleared sample along the plane of light incidence. The mechanical stretch was applied to the short end of the sample using gravitational force and a system of pulleys. No extra alignment of the sample was performed during the experiment in order to record the real-time polarization change during all three stages of the experiment without any external influence. The measurements were done every 5 min; the measured Stokes vectors were averaged throughout the scanning area and their changes in time were analyzed.
3.
Results and Discussion
3.1.
Model Experiments: Variation of Source–Detector Separation
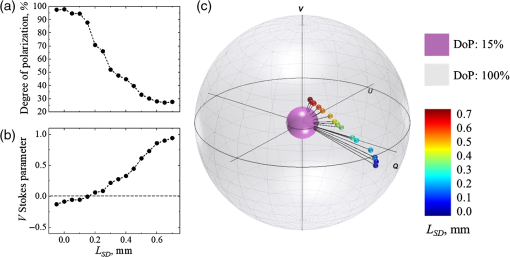
In the experiment with variation of the source–detector separation, LSD, the Stokes vectors of light scattered from a tissue phantom were measured at different LSD. Results of the experiment are presented in Fig. 2: (a) degree of polarization (DoP), (b) V Stokes parameter, (c) Stokes vectors mapped on the Poincaré sphere with respect to the DoP. In panel (c), the radii of the outer (gray) and inner (purple) spheres correspond to 100% and 15%, respectively. The incident light polarization, 100% right circular (Stokes vector [1;0;0;1]), is located at the north pole on the surface of the outer Poincaré sphere. The black lines connecting the origin with the tips of the Stokes vectors correspond to the DoP. Video 1 (mp4, 4 MB) shows the Poincaré sphere rotating around V axis for the better understanding of the positions of the Stokes vectors tips inside the Poincaré sphere.
3.2.
Model Experiments: Phase Alterations Due to Scattering and Birefringence
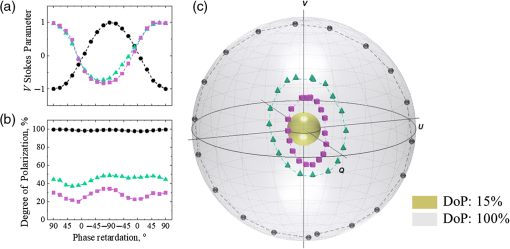
In order to explore alterations of the phase of circularly polarized light due to changes in scattering and birefringence, experiments with a mirror (no scattering) and two scattering phantoms were performed. The state of polarization of light reflected from the mirror and backscattered from the phantoms with different scattering coefficients (μs=4 and 8mm−1) is shown in Fig. 3: (a) V Stokes parameter, (b) DoP, and (c) Stokes vectors mapped on the Poincaré sphere with respect to the DoP. The incident light polarization, right circular, corresponds to the north pole on the Poincaré sphere and 90 deg phase retardation between orthogonal polarization components. Video 2 (mp4, 4 MB) demonstrates the Poincaré sphere from panel (c) rotating around V Stokes axis for the better understanding of location of the Stokes vectors inside the Poincaré sphere.
3.3.
Contributions of Scattering and Birefringence in Phase Alterations Observed in Chicken Skin
In the experiments with chicken skin, scattering was reduced by optical clearing, whereas form birefringence was induced by applying mechanical stretch to the chicken skin sample. An independent measurement of the optical properties of chicken skin tissue with and without optical clearing using a spectrophotometric system43,44 has shown that after optical clearing, the scattering coefficient of chicken skin μs has decreased by 30% (from 13 to 9mm−1), whereas the anisotropy factor g has increased by 18% (from 0.8 to 0.95).
The alignment of collagen fibers in optically cleared chicken skin sample due to mechanical stretch was validated using the SHG imaging. Figure 4 illustrates SHG imaging of collagen fibers of roughly the same area of the sample influenced by different degrees of stretch: (a) no stretch, (b) stretching force of 0.74 N, and (c) stretching force of 1.35 N. As one can see in Fig. 4(a), the collagen bundle without any applied stretch was dispersed; however, after 0.74 N of stretch, it became more aligned and the SHG signal became brighter [see Fig. 4(b)]; after 1.35 N of stretch, this tendency became more prominent [see Fig. 4(c)]. The higher contrast of the fibers at higher degrees of stretch in SHG images correlates with the stronger SHG signal and additionally indicates the higher alignment of the fibers. The direction of the fiber alignment coincided with the direction of the applied stretching force.
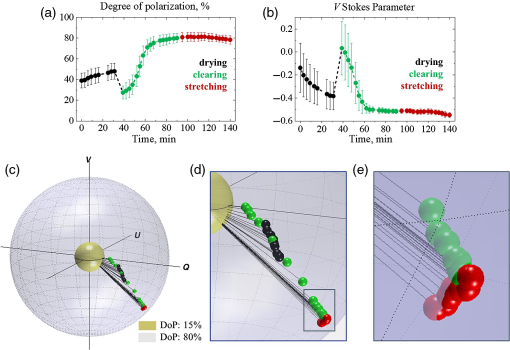
Following the results of model experiments and spectrophotometric and SHG measurements of chicken skin, the three-stage experiments with samples of chicken skin were performed. The alterations of the state of polarization of light propagated within the sample of chicken skin being kept under normal conditions for 30 min (drying) and influenced by optical clearing during 1 h and mechanical stretch (up to 1.5 N) are presented in Fig. 5. Panels (a) and (b) show alterations of the DoP and V Stokes parameter in time; panel (c) illustrates trajectory of measured Stokes vector mapped on the Poincaré sphere: inner (yellow) and outer (blue) spheres correspond to 15% and 80% DoP, respectively; panel (d) shows an enlarged view of the Stokes vector track mapped on the Poincaré sphere; panel (e) shows closely the data points that correspond to the stretching. Each of the data points corresponds to the value of the Stokes vector component averaged over the scanning area (2×2mm2, 200-μm step, 10 measurements at each step) and the error bars represent the standard deviation. For the details of the Q and U Stokes vector components, refer to Fig. S1 in the Supplemental Material.
Following the results of experiments with variation of the source–detector separation (Sec. 3.1), the LSD was set to 0.3 mm, as this was the largest value of separation that provided sufficient DoP (at least 40%). Sufficient DoP in the beginning of the experiment was necessary as the experimental protocol did not allow any extra alignment of the sample during the measurements in order to record the real-time polarization change without any external influence. Alterations of the Stokes vector while the DoP was lower than 20% were not considered reliable.
As one can see in Fig. 5(a), the DoP was ∼40% in the beginning of the experiment. The process of drying caused a growth of the DoP up to 50%, which was likely due to the reduction of scattering of the tissue sample in virtue of its shrinking.51 Once the optical clearing agent was applied topically to the skin tissue, the DoP dropped significantly due to matching of the refractive index on surface of the medium and activation of the impact of photons with longer pathlengths in the tissue to the measured signal.52 Further, during the optical clearing, the DoP grew exponentially up to 80% until it stopped changing by 80th minute of the experiment. Subsequent application of the mechanical stretch did not cause sufficient change in the DoP, which correlates with the results of the model experiments (Sec. 3.2), as mechanical stretch changed predominantly birefringence on the background of suppressed scattering.
The changes of V Stokes parameter are shown in Fig. 5(b). As one can see, at the beginning of the measurements, the state of polarization of multiply scattered light was close to linear, which means that the detected portions of the light with left- and right-handed helicities were almost equal. The process of drying led to the steady decay of V Stokes parameter, followed by a jump at the moment the optical clearing agent was applied. The diffusion of the optical clearing agent into the skin tissue caused reduction of scattering with the exponential decay of V Stokes parameter until it became asymptotic by 80th minute of the experiment. The mechanical stretch led to the alteration of birefringence in the sample, which was manifested in the renewal of the V Stokes parameter decay [Figs. 5(c)–5(e)]. This correlates with the Stokes vector tracks observed in the model experiments (Sec. 3.2) on a smaller scale, as the sample’s birefringence is minor.
The alteration of the V Stokes parameter in the third stage of the experiment was caused by the fact that the mechanical stretch aligned initially dispersed collagen fibers in a major direction, inducing form birefringence. The linearly oriented structure of collagen fibers in skin could be considered as a system of long dielectric cylinders characterized by the difference in the effective refractive index (Δn) for the light polarized along and perpendicular to the cylinders in the model.4 This indicates that the birefringence induced with the mechanical stretch influenced the state of polarization of the light scattered from the tissue sample. As the incident light polarization was circular, it contained the equal portions of the light polarized in parallel and perpendicular directions with respect to the optic axis of the collagen fibers structure. The retardance of one of these polarization components influenced the ellipticity of the resultant polarization, which changed the value of VStokes vector component.
Though in 2D graphs in Figs. 5(a) and 5(b), changes due to mechanical stretch do not appear significant, the mapping of the Stokes vector on the Poincaré sphere allows identifying the nature of these changes [Figs. 5(c)–5(e)] and distinguishing them from changes of the Stokes vector due to variation of scattering. Thus, the Stokes vector alterations associated with drying and optical clearing of the biotissue are manifested as a shift down on the Poincaré sphere accompanied by the increase in the Stokes vector’s magnitude due to simultaneous changes in V Stokes parameter and DoP [Figs. 5(c) and 5(d)], while the Stokes vector alteration due to change in birefringence is observed as a shift on the surface of the Poincaré sphere with the vector’s magnitude preserved [see Fig. 5(e)]. As one can see, the red data points belong to the surface of the same sphere, while the direction of polarization state alterations due to optical clearing (down and toward the surface of the outer sphere) is sufficiently different from the one due to stretching [along the radius of the outer sphere, see Fig. 5(e)]. These results agree well with the results of the model experiments in Sec. 3.2.
The obtained results show that the relative phase δ between two orthogonal polarization components of the electric field of the incident circularly polarized light has changed approximately by 30% as a result of drying, in 4.5 times due to optical clearing and by 1.3% due to mechanical stretch. Changes of the phase retardation during drying and optical clearing are attributed to the variation of scattering. As the scattering was significantly reduced by the optical clearing, the application of mechanical stretch led to the phase retardation associated particularly with the birefringence induced in the sample. According to the obtained results, the birefringence (Δn=δλ/2πl, where λ is the wavelength and l is the photons pathlength within the tissue up to 1 mm53) for the chicken skin sample is estimated at 0.3×10−3. The result agrees well with the results of alternative studies.4 The overall change in the value of birefringence during mechanical stretch (|Δn1−Δn2|=Δδ⋅λ/2πl, where Δδ is the change in the relative phase) is estimated as 3.7×10−6. In fact, the impact of scattering on the DoP and phase alteration prevails significantly the phase shift due to birefringence. Therefore, it is almost impossible to observe the phase changes due to birefringence in skin at normal conditions. In our case, with a reduction of scattering utilizing optical clearing and with enhancement of birefringence by stretching, we were able to observe and assess them.
Thus, the changes of directions of the V Stokes parameter and DoP [see Figs. 5(a) and 5(b)] are associated, respectively, with the changes of anisotropy of scattering of circularly polarized light and the changes of scattering and total internal reflection on the medium boundary due to optical clearing. The impact of scattering on the circularly polarized light was extensively studied and evaluated earlier.22–24,54,55 While the V Stokes parameter and DoP on their own do not bring notable information in terms of distinguishing contributions of scattering and birefringence, the resultant Stokes vector trajectory on the Poincaré sphere [see Fig. 5(c)] allows one to reveal the role of both scattering and birefringence in the total phase retardation.
4.
Summary and Conclusions
The study is focused on the assessment of the isolated contributions of scattering and birefringence in the overall phase retardation of the circularly polarized light propagated through the tissue-like scattering medium. With the help of the model experiments utilizing tissue phantoms, the influence of source–detector separation on the polarimetric response of the medium has been demonstrated. Moreover, the alteration of phase of circularly polarized light due to scattering and birefringence was illustrated using tissue phantoms and chicken skin tissue. In the experiments with chicken skin, it has been found that the phase retardation between two orthogonal electric field components of the circularly polarized light associated with scattering alterations has changed approximately by 30% during 30 min of drying and in 4.5 times during 1 h of optical clearing with the use of 40% solution of glycerol in water. Phase retardation associated with the alteration of birefringence has changed by 1.3% when mechanical stretch up to 1.5 N was applied. The decrease of tissue scattering due to optical clearing enhances the DoP up to 80% that makes birefringence distinguishable on the background of the remaining scattering. Thus, the birefringence, induced by mechanical stretch, is observed as the shift of the Stokes vector on the surface of the Poincaré sphere, whereas reduction of scattering is manifested in the growing magnitude of the Stokes vector, which was validated with model experiments. The overall change in the value of birefringence due to mechanical stretch is estimated as 3.7×10−6. The value of birefringence in chicken skin is estimated to be 0.3×10−3, which agrees well with the known literature data.4
Thus, the isolated contributions of scattering and birefringence in the phase retardation of circularly polarized light propagated in biological tissues have been demonstrated with the help of tissue-mimicking phantoms and chicken skin in vitro with application of the optical clearing and mechanical stretch. The alignment of collagen fibers in chicken skin due to stretch and, therefore, inducement of birefringence were validated by the SHG imaging. The Poincaré sphere is suggested to be used as a graphical tool for observing the trajectories of the Stokes vector for subsequent functional (qualitative) and quantitative characterization of biological tissues and turbid tissue-like scattering medium. The described approach can be beneficial for the more advanced characterization of various types of malformations within biological tissues, e.g., based on combination of Stokes-vector and Mueller-matrix polarimetry. This would allow functional quantitative assessment of phase-dependent Mueller-matrix elements and their interpretation in terms of phase retardation between the electric field components due to scattering and/or birefringence.
Disclosures
The authors declare that there are no conflicts of interests related to this study.
Acknowledgments
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 713606, the ATTRACT project funded by the EC under Grant Agreement 777222, Academy of Finland (Grant Nos: 314369 and 325097), INFOTECH strategic funding, MEPhI Academic Excellence Project (Contract No. 02.a03.21.0005), and National Research Tomsk State University Academic D.I. Mendeleev Fund Program. The authors are grateful to Prof. Valery Tuchin and Prof. Alex Vitkin for critical comments and useful discussions at the stage of the paper preparation.
References
1. T. Novikova et al., “Polarized light for biomedical applications,” J. Biomed. Opt., 21 (7), 071001 (2016). https://doi.org/10.1117/1.JBO.21.7.071001 JBOPFO 1083-3668 Google Scholar
2. N. Ghosh and A. I. Vitkin, “Tissue polarimetry: concepts, challenges, applications, and outlook,” J. Biomed. Opt., 16 (11), 110801 (2011). https://doi.org/10.1117/1.3652896 JBOPFO 1083-3668 Google Scholar
3. V. V. Tuchin, “Polarized light interaction with tissues,” J. Biomed. Opt., 21 (7), 071114 (2016). https://doi.org/10.1117/1.JBO.21.7.071114 JBOPFO 1083-3668 Google Scholar
4. V. V. Tuchin, L. Wang and D. A. Zimnyakov, Optical Polarization in Biomedical Applications, Springer Science & Business Media, Berlin, Heidelberg (2006). Google Scholar
5. R. Azzam, “Stokes-vector and Mueller-matrix polarimetry,” J. Opt. Soc. Am. A, 33 (7), 1396 –1408 (2016). https://doi.org/10.1364/JOSAA.33.001396 JOAOD6 0740-3232 Google Scholar
6. J. F. De Boer, “Polarization sensitive optical coherence tomography,,” Handbook of Coherent-Domain Optical Methods, 857 –888 Springer, New York (2013). Google Scholar
7. F. Vasefi et al., “Polarization-sensitive hyperspectral imaging in vivo: a multimode dermoscope for skin analysis,” Sci. Rep., 4 4924 (2014). https://doi.org/10.1038/srep04924 SRCEC3 2045-2322 Google Scholar
8. T. Yasui, Y. Tohno and T. Araki, “Determination of collagen fiber orientation in human tissue by use of polarization measurement of molecular second-harmonic-generation light,” Appl. Opt., 43 (14), 2861 –2867 (2004). https://doi.org/10.1364/AO.43.002861 APOPAI 0003-6935 Google Scholar
9. S. R. P. Pavani, J. G. DeLuca and R. Piestun, “Polarization sensitive, three-dimensional, single-molecule imaging of cells with a double-helix system,” Opt. Express, 17 (22), 19644 –19655 (2009). https://doi.org/10.1364/OE.17.019644 OPEXFF 1094-4087 Google Scholar
10. D. H. Goldstein, Polarized Light, CRC press, Boca Raton (2016). Google Scholar
11. N. Agarwal et al., “Spatial evolution of depolarization in homogeneous turbid media within the differential Mueller matrix formalism,” Opt. Lett., 40 (23), 5634 –5637 (2015). https://doi.org/10.1364/OL.40.005634 OPLEDP 0146-9592 Google Scholar
12. O. Angelsky et al., “Investigation of 2D Mueller matrix structure of biological tissues for pre-clinical diagnostics of their pathological states,” J. Phys. D: Appl. Phys., 38 (23), 4227 (2005). https://doi.org/10.1088/0022-3727/38/23/014 JPAPBE 0022-3727 Google Scholar
13. N. K. Das et al., “Quantitative assessment of submicron scale anisotropy in tissue multifractality by scattering Mueller matrix in the framework of Born approximation,” Opt. Commun., 413 172 –178 (2018). https://doi.org/10.1016/j.optcom.2017.11.082 OPCOB8 0030-4018 Google Scholar
14. M. Sun et al., “Characterizing the microstructures of biological tissues using Mueller matrix and transformed polarization parameters,” Biomed. Opt. Express, 5 (12), 4223 –4234 (2014). https://doi.org/10.1364/BOE.5.004223 BOEICL 2156-7085 Google Scholar
15. E. Du et al., “Mueller matrix polarimetry for differentiating characteristic features of cancerous tissues,” J. Biomed. Opt., 19 (7), 076013 (2014). https://doi.org/10.1117/1.JBO.19.7.076013 JBOPFO 1083-3668 Google Scholar
16. A. Pierangelo et al., “Ex-vivo characterization of human colon cancer by Mueller polarimetric imaging,” Opt. Express, 19 (2), 1582 –1593 (2011). https://doi.org/10.1364/OE.19.001582 OPEXFF 1094-4087 Google Scholar
17. J. Rehbinder et al., “Ex vivo Mueller polarimetric imaging of the uterine cervix: a first statistical evaluation,” J. Biomed. Opt., 21 (7), 071113 (2016). https://doi.org/10.1117/1.JBO.21.7.071113 JBOPFO 1083-3668 Google Scholar
18. M. Borovkova et al., “Complementary analysis of Mueller-matrix images of optically anisotropic highly scattering biological tissues,” J. Eur. Opt. Soc.-Rapid, 14 (1), 20 (2018). https://doi.org/10.1186/s41476-018-0085-9Google Scholar
19. N. Ghosh, M. F. Wood and I. A. Vitkin, “Mueller matrix decomposition for extraction of individual polarization parameters from complex turbid media exhibiting multiple scattering, optical activity, and linear birefringence,” J. Biomed. Opt., 13 (4), 044036 (2008). https://doi.org/10.1117/1.2960934 JBOPFO 1083-3668 Google Scholar
20. S. Alali, Y. Wang and I. A. Vitkin, “Detecting axial heterogeneity of birefringence in layered turbid media using polarized light imaging,” Biomed. Opt. Express, 3 (12), 3250 –3263 (2012). https://doi.org/10.1364/BOE.3.003250 BOEICL 2156-7085 Google Scholar
21. M. Ahmad et al., “Do different turbid media with matched bulk optical properties also exhibit similar polarization properties?,” Biomed. Opt. Express, 2 (12), 3248 –3258 (2011). https://doi.org/10.1364/BOE.2.003248 BOEICL 2156-7085 Google Scholar
22. B. Kunnen et al., “Application of circularly polarized light for non-invasive diagnosis of cancerous tissues and turbid tissue-like scattering media,” J. Biophotonics, 8 (4), 317 –323 (2015). https://doi.org/10.1002/jbio.201400104Google Scholar
23. C. Macdonald and I. Meglinski, “Backscattering of circular polarized light from a disperse random medium influenced by optical clearing,” Laser Phys. Lett., 8 (4), 324 (2011). https://doi.org/10.1002/lapl.201010133 1612-2011 Google Scholar
24. E. Avci, C. Macdonald and I. Meglinski, “Helicity of circular polarized light backscattered from biological tissues influenced by optical clearing,” Proc. SPIE, 8337 833703 (2012). https://doi.org/10.1117/12.923731Google Scholar
25. M. Borovkova et al., “Influence of scattering and birefringence on the phase shift between electric field components of polarized light propagated through biological tissues,” Proc. SPIE, 11075 110750R (2019). https://doi.org/10.1117/12.2526394 PSISDG 0277-786X Google Scholar
26. I. Meglinski et al., “Screening cancer aggressiveness by using circularly polarized light,” in Opt. in the Life Sci., OSA Technical Digest (online), BM2A.4 (2013). Google Scholar
27. I. Meglinski et al., “The mapping of tissues scattering properties on the Poincaré sphere,” in Biomed. Opt., OSA Technical Digest, BW3B.6 (2012). Google Scholar
28. S. L. Jacques, “Optical properties of biological tissues: a review,” Phys. Med. Biol., 58 R37 –R61 (2013). https://doi.org/10.1088/0031-9155/58/11/R37 PHMBA7 0031-9155 Google Scholar
29. S. Alali and I. A. Vitkin, “Polarized light imaging in biomedicine: emerging Mueller matrix methodologies for bulk tissue assessment,” J. Biomed. Opt., 20 (6), 061104 (2015). https://doi.org/10.1117/1.JBO.20.6.061104 JBOPFO 1083-3668 Google Scholar
30. J. C. Mansfield et al., “Collagen fiber arrangement in normal and diseased cartilage studied by polarization sensitive nonlinear microscopy,” J. Biomed. Opt., 13 (4), 044020 (2008). https://doi.org/10.1117/1.2950318 JBOPFO 1083-3668 Google Scholar
31. J. F. De Boer et al., “Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography,” Opt. Lett., 22 (12), 934 –936 (1997). https://doi.org/10.1364/OL.22.000934 OPLEDP 0146-9592 Google Scholar
32. S. H. Hussain, B. Limthongkul and T. R. Humphreys, “The biomechanical properties of the skin,” Dermatolog. Surg., 39 (2), 193 –203 (2013). https://doi.org/10.1111/dsu.12095Google Scholar
33. X. Feng, R. Patel and A. N. Yaroslavsky, “Wavelength optimized cross-polarized wide-field imaging for noninvasive and rapid evaluation of dermal structures,” J. Biophotonics, 8 (4), 324 –331 (2015). https://doi.org/10.1002/jbio.201400105Google Scholar
34. F. MacKintosh et al., “Polarization memory of multiply scattered light,” Phys. Rev. B, 40 (13), 9342 (1989). https://doi.org/10.1103/PhysRevB.40.9342Google Scholar
35. M. Xu and R. Alfano, “Circular polarization memory of light,” Phys. Rev. E, 72 (6), 065601 (2005). https://doi.org/10.1103/PhysRevE.72.065601Google Scholar
36. V. Kuzmin and I. Meglinski, “Helicity flip of the backscattered circular polarized light,” Proc. SPIE, 7573 75730Z (2010). https://doi.org/10.1117/12.841193Google Scholar
37. D. Bicout et al., “Depolarization of multiply scattered waves by spherical diffusers: Influence of the size parameter,” Phys. Rev. E, 49 (2), 1767 (1994). https://doi.org/10.1103/PhysRevE.49.1767Google Scholar
38. Y. L. Kim et al., “Circular polarization memory effect in low-coherence enhanced backscattering of light,” Opt. Lett., 31 (18), 2744 –2746 (2006). https://doi.org/10.1364/OL.31.002744 OPLEDP 0146-9592 Google Scholar
39. J. F. Ribeiro et al., “Skin collagen fiber molecular order: a pattern of distributional fiber orientation as assessed by optical anisotropy and image analysis,” PLoS One, 8 (1), e54724 (2013). https://doi.org/10.1371/journal.pone.0054724 POLNCL 1932-6203 Google Scholar
40. V. V. Tuchin, “Tissue optics: light scattering methods and instruments for medical diagnostics,” SPIE Press, Bellingham, Washington (2007). Google Scholar
41. M. Ferraro et al., “Observation of polarization-maintaining light propagation in depoled compositionally disordered ferroelectrics,” Opt. Lett., 42 3856 –3859 (2017). https://doi.org/10.1364/OL.42.003856 OPLEDP 0146-9592 Google Scholar
42. M. S. Wróbel et al., “Use of optical skin phantoms for preclinical evaluation of laser efficiency for skin lesion therapy,” J. Biomed. Opt., 20 (8), 085003 (2015). https://doi.org/10.1117/1.JBO.20.8.085003JBOPFO 1083-3668 Google Scholar
43. M. S. Wróbel et al., “Measurements of fundamental properties of homogeneous tissue phantoms,” J. Biomed. Opt., 20 (4), 045004 (2015). https://doi.org/10.1117/1.JBO.20.4.045004 JBOPFO 1083-3668 Google Scholar
44. S. A. Prahl, M. J. van Gemert and A. J. Welch, “Determining the optical properties of turbid media by using the adding–doubling method,” Appl. Opt., 32 (4), 559 –568 (1993). https://doi.org/10.1364/AO.32.000559 APOPAI 0003-6935 Google Scholar
45. V. Tuchin, “Optical clearing of tissues and blood using the immersion method,” J. Phys. D Appl. Phys., 38 (15), 2497 (2005). https://doi.org/10.1088/0022-3727/38/15/001Google Scholar
46. X. Wen et al., “In vivo skin optical clearing by glycerol solutions: mechanism,” J. Biophotonics, 3 (1–2), 44 –52 (2010). https://doi.org/10.1002/jbio.200910080Google Scholar
47. A. Doronin, C. Macdonald and I. V. Meglinski, “Propagation of coherent polarized light in turbid highly scattering medium,” J. Biomed. Opt., 19 (2), 025005 (2014). https://doi.org/10.1117/1.JBO.19.2.025005JBOPFO 1083-3668 Google Scholar
48. W. Cai et al., “Analytical cumulant solution of the vector radiative transfer equation investigates backscattering of circularly polarized light from turbid media,” Phys. Rev. E, 74 (5), 056605 (2006). https://doi.org/10.1103/PhysRevE.74.056605Google Scholar
49. K. G. Phillips et al., “Time-resolved ring structure of circularly polarized beams backscattered from forward scattering media,” Opt. Express, 13 (20), 7954 –7969 (2005). https://doi.org/10.1364/OPEX.13.007954 OPEXFF 1094-4087 Google Scholar
50. V. Kuzmin and I. Meglinski, “Anomalous polarization effects during light scattering in random media,” J. Exp. Theor. Phys., 110 (5), 742 –753 (2010). https://doi.org/10.1134/S1063776110050031 JTPHES 1063-7761 Google Scholar
51. A. Bykov et al., “Imaging of subchondral bone by optical coherence tomography upon optical clearing of articular cartilage,” J. Biophotonics, 9 (3), 270 –275 (2016). https://doi.org/10.1002/jbio.201500130Google Scholar
52. I. Meglinski et al., “Study of the possibility of increasing the probing depth by the method of reflection confocal microscopy upon immersion clearing of near-surface human skin layers,” Quantum Electron., 32 (10), 875 –882 (2002). https://doi.org/10.1070/QE2002v032n10ABEH002309 QUELEZ 1063-7818 Google Scholar
53. A. Doronin and I. Meglinski, “Online object oriented Monte Carlo computational tool for the needs of biomedical optics,” Biomed. Opt. Express, 2 (9), 2461 –2469 (2011). https://doi.org/10.1364/BOE.2.002461BOEICL 2156-7085 Google Scholar
54. I. Meglinski and V. L. Kuzmin, “Coherent backscattering of circularly polarized light from a disperse random medium,” PIER M, 16 47 –61 (2011). https://doi.org/10.2528/PIERM10102106Google Scholar
55. C. M. Macdonald, S. L. Jacques and I. Meglinski, “Circular polarization memory in polydisperse scattering media,” Phys. Rev. E, 91 (3), 033204 (2015). https://doi.org/10.1103/PhysRevE.91.033204Google Scholar
Biography
Mariia Borovkova is a doctoral candidate at the University of Oulu at the I4Future doctoral program under Marie Skłodowska-Curie fellowship. She received her BS degree in photonics from the ITMO University (St. Petersburg, Russia) in 2014. She obtained a MS degree in optics from the University of Rochester, Rochester, New York, USA and a MS in photonics from the ITMO University in 2016. Her research interests are in polarization-based and spectroscopic imaging for biomedical diagnostics. She is a member of SPIE.
Alexander Bykov is an adjunct professor and biophotonics group leader in the Optoelectronics and Measurement Techniques Unit of the University of Oulu, Finland. He received his PhD from Lomonosov Moscow State University, Russia, and DSc (Tech.) degree from the University of Oulu in 2010. He is an author and coauthor of over 100 papers in peer-reviewed scientific journals. His scientific interests are in the area of noninvasive optical diagnostics including polarization and hyperspectral imaging.
Alexey Popov is a research professor at VTT Technical Research Centre of Finland. His scientific activity covers photonics and nanotechnology, focusing on the development of optical sensors and modalities for biomedical diagnostics, quality of agricultural products and environmental conditions, UV protection, gas sensing, and photocatalysis.
Igor Meglinski is a professor at the University of Oulu (Finland) and Aston University (UK). His research interests lie at the interface between physics and life sciences, focusing on the development of new noninvasive imaging diagnostic techniques in medicine, biology, food sciences, environmental monitoring, and health care industries. He is a chartered physicist (CPhys), chartered engineer (CEng), senior member of IEEE, fellow of Institute of Physics (FInstP), and fellow of SPIE.© The Authors. Published by SPIE under a Creative Commons Attribution 4.0 Unported License. Distribution or reproduction of this work in whole or in part requires full attribution of the original publication, including its DOI. Citation Download CitationMariia A. Borovkova, Alexander V. Bykov, Alexey Popov, and Igor V. Meglinski “Role of scattering and birefringence in phase retardation revealed by locus of Stokes vector on Poincaré sphere,” Journal of Biomedical Optics 25(5), 057001 (20 May 2020). https://doi.org/10.1117/1.JBO.25.5.057001Received: 22 October 2019; Accepted: 27 April 2020; Published: 20 May 2020